definisjon av en slik teorem
I det 5. århundre f.Kr. var det en intellektuell bevegelse på Hellas territorium som kan betraktes som begynnelsen på rasjonell tanke og vitenskapelig mentalitet. En av tenkerne som ledet det nye intellektuelle kurset, var Thales of Miletus, som regnes som den første før-sokratiske, tankestrømmen som brøt med mytisk tenkning og tok de første skrittene i filosofisk og vitenskapelig aktivitet.
De opprinnelige verkene til Thales er ikke bevart, men gjennom andre tenkere og historikere er hans viktigste bidrag kjent: han spådde solformørkelsen i 585 f.Kr. C, forsvarte ideen om at vann er det opprinnelige elementet i naturen og stod også ut som en matematiker, og hans mest anerkjente bidrag var setningen som bærer navnet hans. Ifølge legenden kommer inspirasjonen til teoremet fra Thales 'besøk i Egypt og bildet av pyramidene.
Thales setning
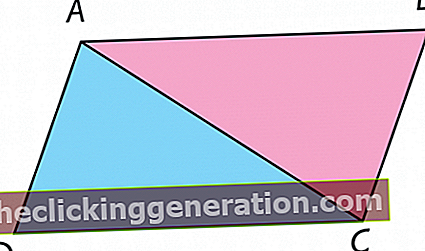
Teoremets grunntanke er enkel: to parallelle linjer krysset av en linje som skaper to vinkler. Dette er to vinkler som er kongruente, det vil si at begge vinklene har samme mål (de er også kjent som tilsvarende vinkler, den ene er på utsiden av parallellene og den andre er på innsiden).
Det må tas i betraktning at det noen ganger er to Thales-teoremer (den ene refererer til lignende trekanter og den andre refererer til de tilsvarende vinklene, men begge setningene er basert på det samme matematiske prinsippet).
Spesifikke applikasjoner
Den geometriske tilnærmingen til Thales teorem har åpenbare praktiske implikasjoner. La oss se det med et konkret eksempel: en 15 m høy bygning kaster en 32 meter skygge og i samme øyeblikk kaster en person en 2,10 meter skygge. Med disse dataene er det mulig å kjenne høyden til individet, siden det må tas i betraktning at vinklene som kaster skygge er kongruente. Med dataene i problemet og prinsippet til Thales 'setning om de tilsvarende vinklene er det således mulig å kjenne individets høyde med en enkel regel på tre (resultatet vil være 0,98 m).
Ovennevnte eksempel illustrerer tydelig at Thales teorem har svært varierte anvendelser: i studiet av geometriske skalaer og metriske forhold mellom geometriske figurer. Disse to spørsmålene om ren matematikk projiseres på andre teoretiske og praktiske sfærer: i utarbeidelsen av planer og kart, i arkitektur, jordbruk eller ingeniørfag.
Som konklusjon kunne vi huske et merkelig paradoks: at selv om Thales fra Miletus levde for 2600 år siden, fortsetter teoremet hans å bli studert fordi det er et grunnleggende prinsipp for geometri.
Foto: iStock - Rawpixel Ltd.
