definisjon av ligning
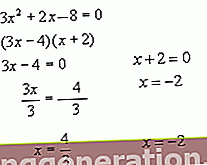I matematikk kalles likheten mellom to algebraiske uttrykk en ligning, som vil bli kalt medlemmer av ligningen. I ligninger vil de virke relatert gjennom matematiske operasjoner, tall og bokstaver (ukjente).
De fleste matematiske problemer finner forholdene uttrykt i form av en eller flere ligninger.
I mellomtiden, når noen av verdiene til variablene i ligningen oppfyller likhet, vil denne situasjonen bli kalt løsningen på ligningen.
Før en ligning kan følgende scenarier oppstå, at ingen av verdiene til det ukjente når likhet, eller tvert imot, at alle mulige verdier av det ukjente oppfyller det, i dette tilfellet vil vi bli møtt med det som kalles identiteter i matematikk og når to matematiske uttrykk faller sammen i ulikheten, vil den bli bestemt som ulikhet.
Det er forskjellige typer ligninger, blant dem finner vi den funksjonelle ligningen, som er en der konstanter og variabler som er involvert ikke er reelle tall, men funksjoner. Når en differensialoperatør dukker opp i noen av medlemmene, kalles de differensiallikninger. Så er det polynomligningen, som vil være den som etablerer likheten mellom to polynomer. På den annen side er førstegradsligninger de der variabelen x ikke heves til noen kraft, hvor 1 er dens eksponent. I mellomtiden er det karakteristiske og differensielle trekket ved ligninger kjent som andregradsligninger at de vil ha to mulige løsninger på det.
Men for astronomi, hvor begrepet også sier nåværende, er en ligning forskjellen mellom sted eller gjennomsnittlig bevegelse og den sanne eller tilsynelatende som en stjerne har.
